素数筛 与 线性筛

素数筛

使用n + 1长度的数组p 表示0～n位的质数情况。0代表质数，1代表合数。

将数组每一位均初始化为0。

已知0、1为非质数，所以从2开始考虑。

从2开始依次处理2～n的每一位i，如果被处理的数已被标记为合数，则跳过本次处理。

获取i的2倍、3倍、4倍…，记为j，将j标记为合数。

p中2～n中标记为0的数，均为质数。

---

代码示例：统计所有小于非负整数 n 的质数的数量。

/**
 * @param {number} n
 * @return {number}
 */
var countPrimes = function(n) {
    // 素数筛 0:素数 1:非素数
    let p = new Array(n + 1).fill(0);
    for (let i = 2; i < n; i++) {
        if (p[i] === 1) continue;
        for (let j = i * i; j < n; j += i) { // 剪枝： i * i 之前的都已经标记过了
            p[j] = 1;
        }
    }
    let cnt = 0;
    for (let i = 2; i < n; i++) {
        if (p[i] === 0) cnt++;
    }

    return cnt;
};

线性筛

也叫“欧拉筛”，时间复杂度为O(n)。

核心思想：每个合数，仅被它的最小质因子筛去。

代码示例-法1：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <queue>
#include <stack>
#include <algorithm>
#include <string>
#include <map>
#include <set>
#include <vector>
using namespace std;
#define MAXN 10000
int prime[MAXN]; // 存放素数
int tag[MAXN] = {0}; // 第i个数是否为素数 0素数 1合数

// 线性筛 求素数个数
int init_prime(int n) {
    int cnt = 0;
    tag[0] = tag[1] = 1; // 0和1都是合数
    for (int i = 2; i < n; i++) {
        if (tag[i] == 0) {
            prime[cnt++] = i; // 标记i为质数
        }
        for (int j = 0; j < cnt && i * prime[j] < n; j++) {
            tag[i * prime[j]] = 1; // i与所有小于i的质数相乘 将结果都标记为合数
            if (i % prime[j] == 0) break; // 剪枝：每个合数，仅被它的最小质因子标记一次
        }
    }
    cout << n << "以内素数的个数为：" << cnt << "个。" << endl; 
    return cnt;
}

int main() {
    int n;
    cin >> n;
    init_prime(n);
    for (int i = 0; i < n; i++) {
        if (tag[i] == 0) cout << i << "为素数" << endl;
    }
    return 0;
}

代码示例-法2:

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <queue>
#include <stack>
#include <algorithm>
#include <string>
#include <map>
#include <set>
#include <vector>
using namespace std;
#define MAX_N 50000
// prime[0]: 素数的数量 = n
// prime[i]: i ∈ [1, n]时 表示第i个素数的值
long long prime[MAX_N + 5] = {0}; 
void init_prime() {
    for (long long i = 2; i <= MAX_N; i++) {
        if (!prime[i]) { // 当前为素数 没有被标记为1
            prime[++prime[0]] = i; 
        }
        for (long long j = 1; j <= prime[0]; j++) {
            if (i * prime[j] > MAX_N) break;
            prime[i * prime[j]] = 1; // 将prime[合数] 标记为1
            if (i % prime[j] == 0) break;
        }
    }
    return ;
}

线性筛图解：

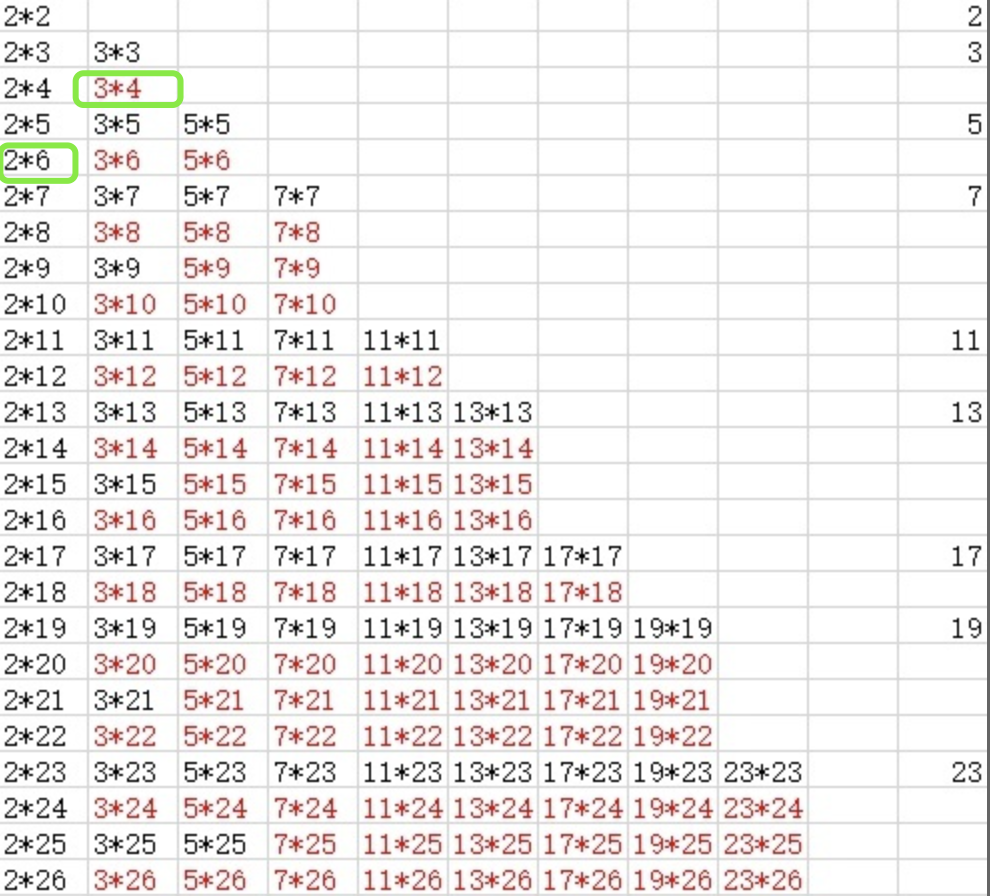
线性筛合数标记的剪枝原理：

合数 只能被其最小质因子 标记一次。

1. 当 i = 4，j = 2 时，j 可以整除 i，即 j * N = i， 此时可知 j 是 i 的质因子。
2. 当 i = 4，j + 1 = 3 时，合数为 i * (j + 1) = 12， 因为 j 是 i 的因子，所以 (j * N) * (j + 1)= 12， 即 质数 j 也是 合数12 的质因子。
3. 因为 j < (j + 1)，所以可证得合数12的最小质因子不是 j + 1。