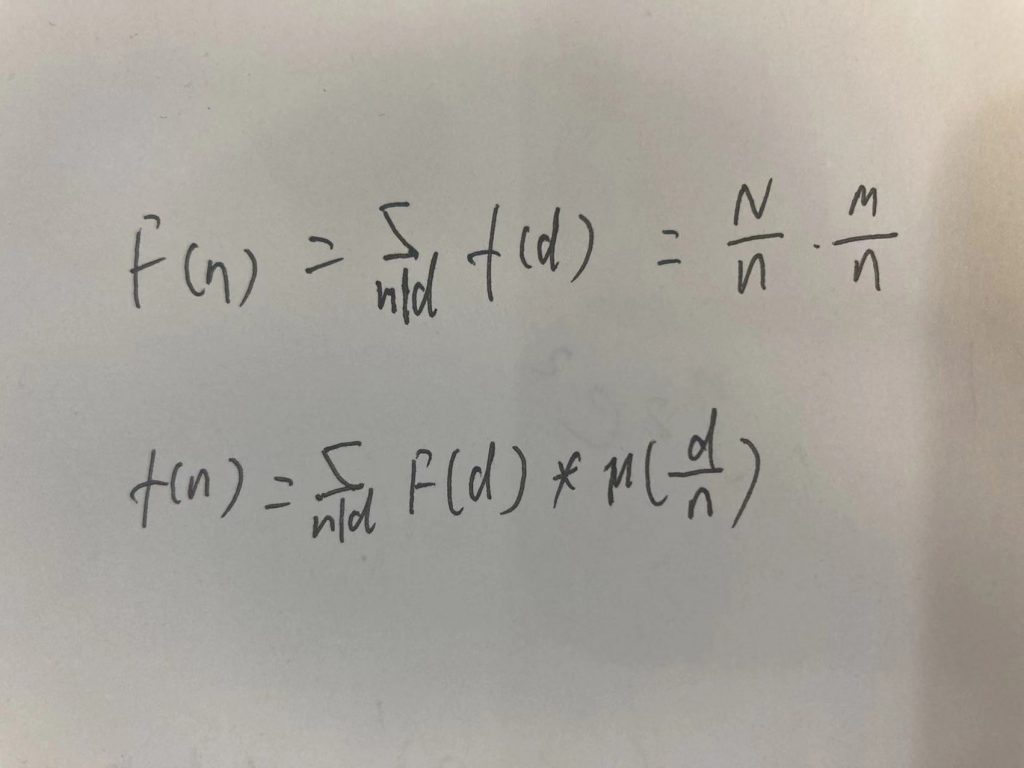莫比乌斯反演

莫比乌斯函数

μ(n) ——默比乌斯函数，关于非平方数的质因子数目。

莫比乌斯函数完整定义的通俗表达：

1. 莫比乌斯函数μ(n)的定义域是N；
2. μ(1)=1；
3. 当n存在平方因子时，μ(n)=0；
4. 当n是素数或奇数个不同素数之积时，μ(n)=-1；
5. 当n是偶数个不同素数之积时，μ(n)=1。

莫比乌斯函数高效预处理代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <queue>
#include <stack>
#include <algorithm>
#include <string>
#include <map>
#include <set>
#include <vector>
using namespace std;

#define MAX_N 10000
int mu[MAX_N + 5] = {0}; // mu[i]: i位置的莫比乌斯函数值
int prime[MAX_N + 5] = {0}; // prime[i]: 标记i是不是素数

// 线性筛 O(n)
void init_prime(int n) {
    mu[1] = 1;
    for (int i = 2; i <= n; i++) {
        if (!prime[i]) {
            prime[++prime[0]] = i;
            mu[i] = -1; // 素数的莫比乌斯函数值为-1
        }
        for (int j = 1; j <= prime[0]; j++) {
            if (i * prime[j] > n) break;
            prime[i * prime[j]] = 1; // i 和 最小质数相乘 结果标记为合数
            if (i % prime[j] == 0) break; // 每个合数，仅被它的最小质因子筛去。
            mu[i * prime[j]] = -mu[i]; 
        }
    }
    return ;
}

int main() {
    int n;
    cin >> n;
    init_prime(n);
    for (int i = 1; i <= n; i++) {
        cout << "mu[" << i << "] = " << mu[i] << endl;
    }
    return 0;
}

莫比乌斯函数的性质：

前提：d是n的所有因子。

1. 所有d的莫比乌斯函数值之和，为0
2. 当且仅当n等于1时，为1

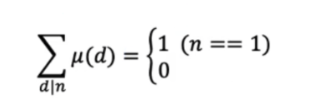
狄利克雷卷积

l() ‘卷’ g() = l(d) * g(n/d) [n的所有因子d的累加]

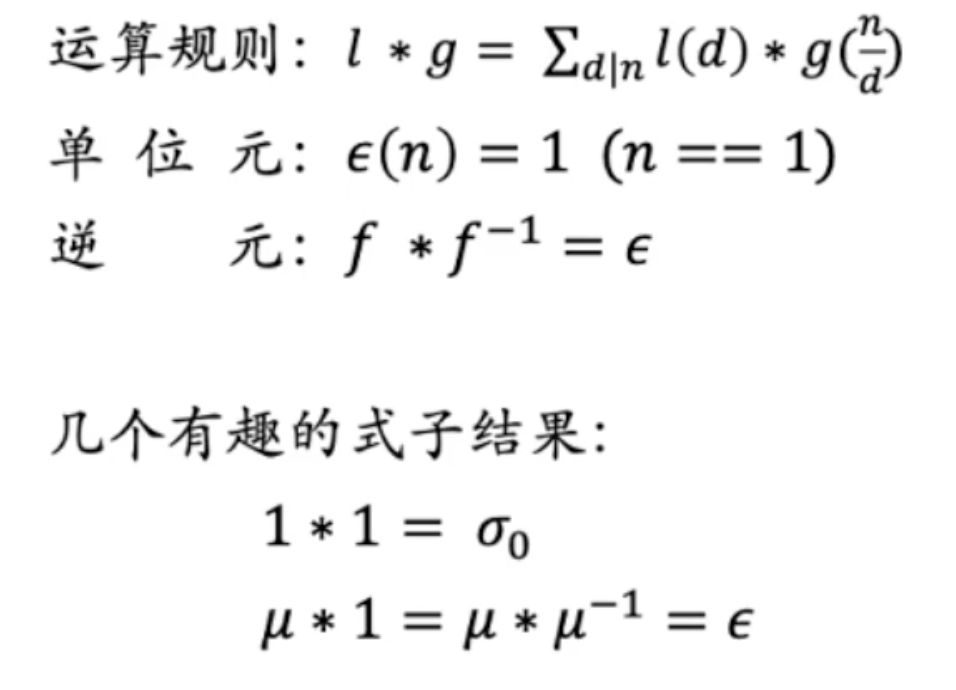
莫比乌斯反演

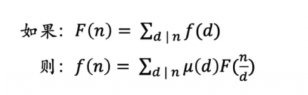
莫比乌斯反演的意义：

莫比乌斯反演，提供了一种文体转化能力

实际上，大多数的算法设计，就是在进行问题形式的转化

莫比乌斯反演的演示题

给定N，M，求 1<=x<=N , 1<=y<=M 且gcd(x, y)为质数的(x， y)有多少对？

• F(n)为gcd(x,y) 是n的倍数的(x,y)的对数
• f(n)为gcd(x,y) 是n的(x,y)的对数

F(n)好求，f(n)不好求，进行问题转化：